Many modern ion optic elements utilize time-varying electric fields to focus ion beams.  Moreover, they utilize collisional cooling to further focus the ion beam, working better in moderate vacuum than they do in high vacuum.  While these elements can be quite powerful, they require somewhat complex control electronics to generate multiple phases of RF and often DC gradients.  There are simpler focusing elements that utilize electrostatic fields to focus ion beams.  Among these, the most common is the so-called "Einzel Lens".

Basic Geometry

An Einzel lens is comprised of three metal cylinders/electrodes arranged coaxially in a row.  The first and third electrodes have the same voltage applied to them, while the second electrode has a voltage that is "uphill" to ions of the polarity of interest.  For example, if one wants to focus positive ions, then the second electrode will have a voltage that is more positive than the first and second electrodes.

Focusing Mechanism

An Einzel lens works via a semi-delicate balance of ion kinetic energy and the potential difference between the central electrode and the outer electrodes.  As an ion is exiting the first electrode, the uphill electric field slows its axial kinetic energy and also begins to push the ion outward radially.  However, as the ion climbs the uphill potential and slows down as it enters the second electrode, the electric field begins to push the ion inward radially.  The inverse process happens as the ion exits the second electrode.  It feels an inward radial force as it's exiting the second electrode and starts to fall down a "downhill" electric field.  As the ion is entering the third electrode it slows down and feels an outward radial force.  So the overall process is this:

1. Exiting first electrode: ion decelerates axially and is pushed outward radially
2. Entering second electrode: ion continues to decelerate axially (albeit at a slower rate) and is pulled inward radially
3. Exiting second electrode: ion accelerates axially while still being pulled inward radially
4. Entering third electrode: ion continues to accelerate axially (albeit at a slower rate) and is pushed outward radially

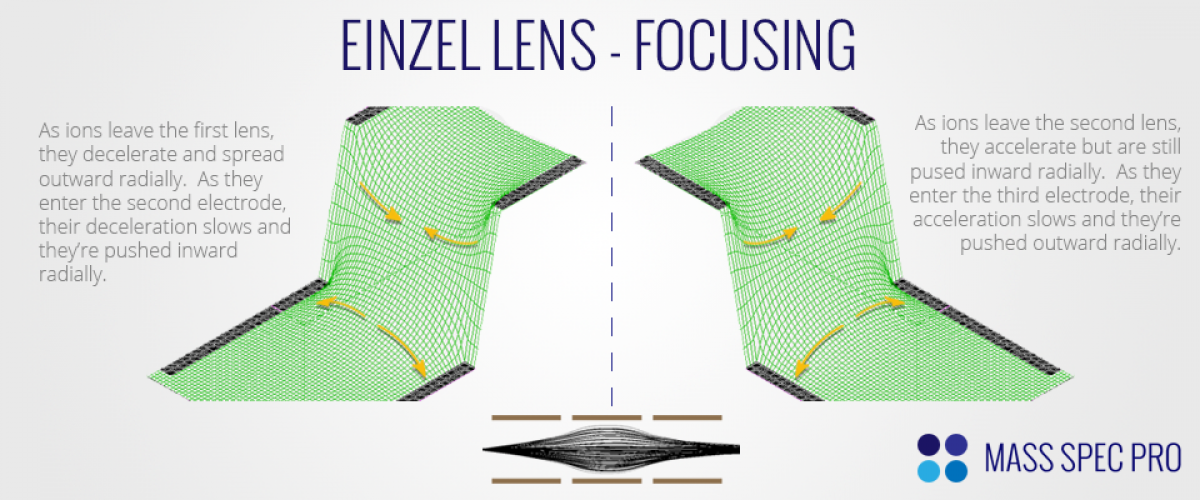
The net effect of these steps is that an ion beam will both slow down and spread outward radially as it starts to pass through the second electrode.  However, while the beam is moving slower through the second lens, it begins to turn back inward radially.  As the beam starts to feel the third electrode, it speeds back up and continues to turn back inward radially.  Lastly, as it enters the third electrode the beam's acceleration slows and the radial compression slows.  Because the ions were moving slower while in the center electrode, the inner radial force experienced here wins out against the outward radial forces experienced in the first and third electrodes.  The degree to which these inner radial forces win out depends on both the kinetic energy of the incoming ions and the potential difference between the electrodes.  If the potential difference between the first and second electrodes is small relative to the kinetic energy of the ions, the ions will not be slowed very much axially and will not feel very much radial force, resulting in little radial change in ion trajectories.  In this case, a beam that was initially diverging would mostly continue to diverge.  However, as the potential difference of the electrodes begins to approach the initial kinetic energy of the ions, the ions slow down substantially and feel more significant radial forces.  As such, the changes in the radial component of ion motion become more significant.  If the radial forces are significant enough, a beam that was originally diverging can be made to converge:

If the potential difference between the electrodes gets too close to the kinetic energy of the incoming ion beam (or exceeds it), then the ions become very slow and can even turn around as they approach the second electrode.  Obviously this is an undesirable solution for focusing, but it can be practical for gating an ion beam such that it stops passing through an instrument for some duration of time (e.g. during mass analysis).

Dependence on Kinetic Energy And Pressure

Since the focusing mechanism of the Einzel lens relies on a balance between the potential difference of the electrodes and the kinetic energy of the ions, it does not work well when an incoming ion beam has a broad range of kinetic energies.  As such, an Einzel lens should only be used for focusing at a point in the instrument where the kinetic energy of the ion beam is well-controlled (e.g. after thermalizing the ions in an ion guide). 

As with all mechanisms of controlling ions with electrostatic fields, operation at elevated pressures is problematic for Einzel lenses.  This is because any given ion-neutral collision will cause the ion's speed and velocity to change, often in such a way that the electrostatic field can not account for.  As pressure increases, the ions will experience more collisions as they pass through an Einzel lens stack, making it increasingly hard to focus ions.  The main takeaway is that an Einzel lens should only be operated at relatively low pressures:

The pressure range in which an Einzel  lens stack's performance will degrade depends on several factors (e.g. ion kinetic energy, and lens length/radii).  However, it's generally a safe assumption that if you're operating at 1 mTorr or higher, then you're better off using a ion optical element that can provide stronger focusing at elevated pressures (e.g. a multipole ion guide).